In Defense of the Low-Event Players

I made a spreadsheet today. Given a GF/game and a GA/game rate, it simulates the results of 1000 games.

The rates are divided by 60. Then each game is simulated in 60 sections. A different random number is compared to each rate each minute. When the GF random number is lower than the GF/minute rate, a goal for is counted for that minute. Same goes for the GA. The GF and GA are totalled up after 60 minutes to produce a game score. If the score is tied at the end of 60, it is counted as a tie.

I had a couple of objectives. First, I wanted to test my belief that a given positive goal differential is more meaningful in a low-scoring environment than in a high-scoring environment.

I ran the simulation for ten times for a total of 10,000 games for six different GF/GA rate pairings.


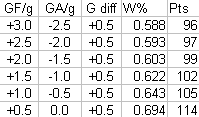
The pts column is simply the number of points this w% would correspond to in an 82-game season.

The difference is not as pronounced as I expected. This is probably due to the increasing liklihood of ties in low-scoring games.

Secondly (and more importantly), I wanted to test the effects of situational changes to a team's GF/GA rates mid-game. To do this, I set up columns for running game scores with initial GF/GA rates (i.e. +3.5/-3.0), and more conservative GF/GA rates (i.e. +1.0/-1.0).

Then I added a hybrid column that started out with the 'initial' GF/GA rates. When the team had a lead, they would switch to the conservative rates. If they were tied or behind, they would switch back to their initial game plan.



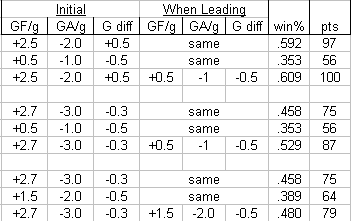
In the first example (first three rows of the table), the team plays initially with GF/GA rates of +2.5/-2.0 for a goal differential of +0.5. Playing this way all the time would lead to a .592 win%. This team can also play a shut-down style, producing +0.5/-1.0. If they played this way all the time, they would have a win% of .353.

However, if this team started out with their first rate, then switched to their shut-down rates whenever they had a lead, their win% jumped to .609. There are situations when a negative goal differential can be better than a positive goal differential.

This is a dumb simulation, too - if the team took a 1-0 lead in the first minute, it would unwisely switch to the low rates until the opponent tied it up. If it were built to gradually change to the most defensive style or only do so in the 3rd period, it would probably produce even better results.

In the second and third examples the effect is more pronounced. At it's best, this team can only produce a +2.7/-3.0 for a differential of -0.3. They can play the same shutdown style as the first team, +0.5/-1.0. Although both styles produce a negative differential, when used in unison they can produce a winning team. Weird.

In the third example, the team's initial rates are +2.7/-3.0 again, but can only manage +1.5/-2.0 when playing defensively. I added this option in case a +0.5/-1.0 style is beyond the realm of possibility. Even so, the team sees improvement when switching to the lower-event style although it has an worse differential than their initial gameplan.

So, it is provable that going into a defensive shell has merit. When you're leading, it can be wise to sacrifice two goals from your GF/game rate if it means you can reduce your GA/game rate by one. However, it's not so easy to prove that the defensive games some teams employ actually reduces their GA/game rate significantly.

Also worth mentioning - this simulation only considered one team who could change their style of play. If the team in question fell behind they could still score at their higher rate, giving them an advantage. A more realistic simulation would consider changes to the opponent's style of play as well.

There is a flaw in this simulation technique: The win probabilities are a little low compared to what should be expected (pdf). I believe that could be corrected by tinkering with the sample rate and I don't think this bug should invalidate my conclusions, but I certainly could be wrong (any input, stats gurus?)


In Conclusion

Most statistical analyses break the game up into even strength, PP and PK situations. I think it's clear that game situations - tied, leading, trailing - should also be considered. Players are not robots who simply produce goals for and against at a fixed rate in a Poisson-like distribution regardless of the score. Even if you're a solid plus player against any opposition, it's not smart to play gung ho for the greatest positive goal differential. There are times when a lower GA style - even at the expense of a negative differential - is the preferred way to play. Of course, this is entirely contingent on whether it is even possible for teams/players to change their style in this manner. It's not a given that this is possible. If it is possible and done regularly, then playing when ahead/behind can be a very different game than playing when tied - just like playing on the PP/PK is a different game than playing at ES. I'd be very interested to see stats listing the most effective players in tied game situations.

Now, if you accept that playing low-event game is wise when leading, it also stands to reason that it would be wise to change one's style to a higher-risk game (more GF at the expense of far more GA) when losing games. You see this regularly with pulled goalies.

P.S. This all reminds me of a good discussion over at Tom Benjamin's awhile back (sorry - can't find the exact post) about the relative effectiveness of Ohlund and Jovanovski under different situations. Ohlund was used more when the Canucks were leading while Jovo played more when losing. Jovanovski incurred some additional minuses due to playing a riskier style uinder these circumstances. This made him look bad statistically, but really had a minimal effect on the team's record since they were already losing. It's an excellent illustration of what I'm trying to say in this post.

~~~

Speaking of low-event...

0-0 tie last night. Although no individual player scored any points, the NHL standings system sees fit to distribute three points amongst the teams involved.

Sophie's Gainey's Choice

Which pending UFA does Bob Gainey keep: Andrei Markov or Sheldon Souray?

It's not quite as heart-wrenching as Muckler's Chara/Redden dilemma, but it's a tough decision nonetheless. Complicating matters is heart&soul guy Craig Rivet will also be a UFA come season's end.

Sheldon says Markov should be the top priority. I like the way the big guy thinks. Souray is arguably the most entertaining individual on the team. His strengths are his huge shot and sledgehammer fists. One would expect a player this noticeable to catch the eye of GMs like Doug MacLean, which would drive up his pricetag. Markov on the other hand plays a more passive, less spectacular, and less expensive game. For some insight regarding which type of player is more effective in the salary cap era, take a look at the Buffalo Sabres.

To get a feel for what this trio of defensemen cost to sign, I've made a quick & dirty list of somewhat comparable players who recently signed contracts/extensions. Players in Canadian cities are probably more valid comparisons, since they are paying similar taxes.

Souray comparables, from low-end to high-end:

Joe Corvo - 4 yr, $2.625M per year
Philippe Boucher - 3 years, $2.5M
Jaroslav Spacek - 3 years, $3.3M
Adrian Aucoin - 4 years, $4M
Pavel Kubina - 4 years, $5M

A complicating factor is Souray's huge season currently underway. If he maintains his current pace, he's looking at >$5M. Aucoin is an interesting case. He developed from a one dimensional player - a guy with a great shot - into a renowned workhorse. Remember Aucoin's 98-99 season in Vancouver? 23 goals, 11 assists in 82 games. Souray was never this one-dimensional. He could always fight, too. He may yet turn into a solid defender, but I'm not holding my breath.


Markov comparables:

Mike Van Ryn - 4 years, $2.9M per year
Filip Kuba - 3 years, $3M
Marek Zidlicky - 4 years, $3.35M
Tomas Kaberle - 5 years, $4.25M

Defensemen with Markov's combination of age, experience and numbers are rare. Kaberle has accomplished a bit more, and should provide a ceiling. I'd love to see this guy signed long term. Git 'r' done, Bob!


Rivet Comparables:

Hal Gill - 3 years, $2.075M per
Steve Staios - 4 years, $2.7M
Aaron Ward - 2 years, $2.75M

Another good comp might be Chris Phillips, who will also be eligible for UFA. Rivet is currently making $2.5M. It can be insulting to ask a guy to take a pay cut, so I can't see him taking less than that. He may be popular, but if you're being objective you have to admit that Rivet is an average player. You can't win in a capped environment paying above average salaries to average players. If he is signed, let's hope for a hometown discount.

~~~

From Sabermetric Research:

"The teams owned by institutions or corporations made 12.5% (Leafs), 5.8% (Rangers), 0.3% (Flyers), and 7.6% (Canadiens)."

Yes, the Leafs are making more than the Canadiens. Drycleaning all those Stanley Cup banners really cuts into the profits.

Fun wow

Due to my unwillingness to shell out for exotic TV packages, I couldn't watch Friday's game vs. the Sabres. We made do with Ott/Fla, while tracking updates via message board threads.

A comparison of the degree of insane fanaticism at fan boards of each team (the names have been changed to protect the innocent):

Montreal's

Poster #1:
Another penalty to the Habs... 3rd in a row... Buffalo's all over us. Habs keeps making mistakes.
Come on damnit! Hit them, hurt them, skate harder...
Habs kill the penalty... we're playing with fire. We need to raise our intensity to make Buffalo create turnovers too.
SHOOOOOOT GODAMNIT

Poster #2:
My god, where is the dive call .. that was a joke.

Poster #1:
Ryder hooked Briere... 4th straight Habs penalty.
Habs are always behind the play... they dont look confident at all.
BIIIIIG SAAAAVE HUET!
Just robbed one there. Point blank shot from Drury.

Poster #3:
2nd period is over...
Simply awful!

Poster #1:
Carbo better kick some ass in the locker-room... Habs didnt skate with Buffalo at all there.
Just 3 shots by the Habs in 2nd, and 2 of them were by Lats alone.

Buffalo's

Poster #1:
Walker Evans is feeling much better now; thanks, Poster #2, although he pooped a bit sparkly tonight
He got into some foil wrap while we were at the family Thanksgiving gathering. Nothing large or damaging to him, but it is damn weird to be picking up dog poo with sparkles in it.
Is your wee bairn sleeping a bit better now?

Poster #1:
DAMN DAMN DAMN
1-1; Koivu on a 3-on-2, hon.

Poster #2:
DAMN.
Yeah, the little one is sleeping a little bit better in general, but I think tonight is going to be a long one.
One of my cats got into the easter grass one year and it was sticking out of her ass for like a week. Fun wow.

~~~

Saturday was Red Fisher night in Montreal. Jack Todd and Le Gros Bil documented the affair.

Red has been in the Hockey Hall of Fame for 21 years. He's a living anachronism. Nowadays, I don't know if it's even possible for a journalist to have the kind of relationship Fisher has with the Canadiens organizations and it's players.

He's written millions of words over more than 50 years in the business. I'd wager that not one word of it was gossip. Now that's something to strive for.

~~~

Stu Cowan penned this article about heart health & hockey. It's a subject that hits close to home for me. My Junior High phys ed teacher and former neighbour passed away several years ago after playing a pick-up game.

"MacDonald says he has already received information about three deaths and about seven non-fatal heart attacks."

And that's only one month into the rec season.

"With things like running or cycling, you maintain a steady pace and you can listen to your body when it says slow down or speed up," MacDonald said. "But when you're out for a jog, you don't necessarily need to race down the street with somebody else. But when you're on the ice and the puck is ahead of you and someone else is going for it, you don't think: 'Gee, I wonder what my heart rate is.' You think: 'I'm going to get to that puck first.'

From www.hockeytakesheart.com:

"Have you, a friend or a teammate experienced a heart attack on the ice during or within one hour of playing a hockey game? Medical researchers at the Hockey Takes Heart Study are asking you to contact them with your information through this website or by calling (902) 567-0898."

There is a line at their website that bears repeating:

"Hockey is a great way to stay active, but players should get in shape to play hockey, not play hockey to get in shape."

Saku > Mikko

Thanks, Ottawa, for beating up on the Minnesota Wild for us (Red's recap). I believe it was a hit by Chris Neil that knocked Demitra out of the lineup. The Habs are now 4-0-0 vs. the Northwest division.

It looks like Bonk/Johnson were matched up with Rolston and his wide assortment of linemates. These guys keep facing off against stars and outscoring them. They're bailing out the Koivu and Kovalev lines, who are just treading water at even strength. On top of that, they've been dominant on the PK. Don't look now, but Radek Bonk might just be Montreal's most valuable forward thus far.

Carbonneau dressed seven defensemen last night, and Janne "Two For Holding" Niinimaa was not one of them.

At the start of the season, Niinimaa had this to say about playing in Montreal:

"When people care, you feel that whatever you do out there, good or bad, you're accountable for it. I like that."

Janne should really enjoy this:

So far, the Ribeiro-Niinimaa trade has been a disaster. One of the Habs' biggest problems this year has been staying out of the penalty box. Niinimaa has averaged a minor penalty for every 20.5 minutes of icetime. The rest of the blueline has averaged one for every 42.1 minutes of icetime. The aggressive Mike Komisarek is a distant second place, with a minor every 31.3 minutes.

And the penalties aren't even the most boneheaded thing Niinimaa has done. After having played seven games with his new club, Janne decided to go all Joe Namath and guarantee a win over the best team in the league. Not smart.

What do you do with an 8th string defenseman who's making $2.5M? If you're Dallas, you trade him for Mike Ribeiro. If you're Montreal, you have second thoughts about the price you paid for defensive depth and pine for the days of Karl Dykhuis.

~~~

Who has the better PP point tandem: Toronto or Montreal?

Kaberle + McCabe: 9.0 PP points/60 min
Markov + Souray: 14.8 PP points/60 min

Kaberle + McCabe: $10M in cap space
Markov + Souray: $4.4M in cap space

~~~

Curiosities at the Hockey Recap penalty report:

Georges Laraque's replacement Patrick Thoresen been slapped with 3 instigator penalties already, and Anze Kopitar is guilty of the one and only "face" penalty this season. He must have stuck his tongue out at Blaine Angus.

~~~

Notable Blogosphere activity:

* This headshaking moment is brought to you via BoO (via someone else, via... ad infinitum):

"The Ottawa charter to Philly this afternoon was delayed due to some last-minute culinary demands. The food service caterers were called to deliver a box of chocolate bars, and one player (we don't know who) reportedly demanded a specific type of salad dressing be made available, before the aircraft could depart."

I won't speculate who. I'll just note that known Nancy-boy Jason Spezza does TV spots for "Jubilee Fine Jewellers - Official jeweller of Jason Spezza and the Ottawa Senators." I wonder if Spezza dons a "Jubilee Fine Jewellers" hat prior to post-game interviews.


* At Hockey Analysis, David Johnson reminisces about the time the Leafs traded away the NHL's worst case of acne.


* Spector's Soapbox is a quarterly report of the Eastern Conference.

"MONTREAL CANADIENS. The Habs are off to another good start but unlike last season it doesn't appear they'll suffer a potentially season-threatening collapse."

Yes, the start to this season has been eerily similar to last season. Even all the "Power Rankings" are giving the team lots of love. I'm not quite so optimistic.

Montreal has been winning a lot of close games. They're being outshot regularly. They're -8 at even strength (30GF, 38GA). Special teams have been an excellent +13 (21 ppgf & 6 shgf, 13 ppga & 1 shga), but the rate they've scored shorties can't continue. Their goaltending has arguably been the best in the league, and that is unlikely to continue. Although the rankings say the Habs' schedule has been tough, they haven't played a whole lot of games. They have benefited from plenty of rest.

This is not the second best team in the East.

Some Habs content, for a change

In the last three games involving the Canadiens, there have been 19 goals scored. 18 if you discount an empty netter. Of those 18, 11 were scored on the PP or in the seconds after a penalty expired. Three of those were 5-on-3, or in the seconds after one penalty expired. There was also one SHG.

In three games featuring 19 goals, we've seen a measley six goals scored during 5-on-5 hockey.

Carbonneau, on the arbitrary penalties:

"The penalties are a concern. They're mostly hooking and that's the new NHL. The only thing that bothers me (about the refs) is that there are some other things that aren't being called out there."

In recent games on Sportsnet, the broadcast team hasn't even bothered to try to replay penalty calls. No one can find them.

That's beef #1. Beef #2: that damned puck-over-glass penalty (again).

Two of the those 11 PPGs were a direct result of puck-over-glass minors. One of those was a 5-on-3. Last night's marquee matchup between the Sabres and Sens was decided by puck-over-glass penalties. Ottawa scored on two puck-over-glass PPs and won 4-2 with an empty net goal.

Koivu, on the puck-over glass rule:

"That's the worst rule in hockey."

Imagine if the NFL instituted a rule that made an accidental incomplete pass that goes out of bounds a ten yard penalty, or if the NBA called a foul for an out-of-bounds pass. It is obscenely unjust.

I understand that there are actually some crackpots out there that think this rule is a good idea. Their argument is usually based on the assumption that (1) NHL players should be skilled enough to avoid it or that (2) it forces defensemen to make higher risk plays.

Even if (1) were true (it's obviously not, given the number of these penalties that are called and NOT ONE of them being intentional), the penalty far outweighs the offense. The continuing number of these calls made this season is evidence that (2) is a bad assumption as well. Defensemen still prefer to try to bank it off the glass than send it up the middle, and rightly so. Guess which option will draw more ire from their coach?

There is no way that accidentally throwing a puck over the glass is equivalent to tripping an opponent to prevent a breakaway, or slashing or elbowing or boarding. The puck-over-glass penalty should be reduced to the equivalent of icing, post-haste. Having games decided by 5-on-3 goals because of this rule is no way to introduce new fans to the game.

New NHL hockey is promoted as a exciting, fast skating, back-and-forth game. It's false advertising, because in the last few games I've seen the lasting images are of PP goals scored on unjust or unseen penalties.

~~~

Yea or Nay: The guy featured on the front page of officepools.com is Darren Turcotte.

~~~

There has been lots of press for HOFer Patrick Roy over the last week. As usual, Red's article is the best, hands down.


~~~

Eric Staal went on an early third period high-sticking rampage last night against former his teammates who jumped ship for the Rangers.


~~~

As if the Buffaslug wasn't enough of an eyesore in Buffalo. BfloBlog has added some captivating footage of a dangling bison penis to the top of their page.

~~~

Just because no one else has mentioned it lately: Sidney Crosby is eligible to play for Canada at the WJHCs in Sweden this year. It is my opinion that he will be considered the best player in hockey by the end of this season, and he's still junior-eligible. Wow.

~~~

Some Gazette writers are authoring blogs! Dave Stubbs and Sidhartha Banerjee can bee seen at Habs Inside/Out. For some reason, Mike Boone gets his own page: Mike Boone's Online Eeee-mail.

On the Forecheck - more hockey numbers!

Sabermetric Research has occasional hockey material.

When an a Bad Economist Watches a Hockey Game

Interesting article in the National Post (found via Kukla's, as usual).

"Despite increasing public unease over violence in hockey, a statistical analysis of NHL data by university professors shows that on-ice fighting is a good strategy for team success."

Well, isn't that interesting. And contradictory to current consensus.

At first sniff, it doesn't pass the BS test. While it's possible that instigating a fight may 'spark' one's team to a better performance, how do you distinguish which team is 'sparked?' If the fighting majors are coincidental, shouldn't both teams receive the same benefit? I just had to take a closer look. The paper is available here.

To summarize, Ordinary Least Squares is used to determine which variables contribute positively and negatively to team points and team goals against. Here are their equations:

PTS = a0 +a1(GA) + a2(A) + a3(TFW) + a4(TFL) + a5(PIM) +
a6(MAJORS) + a7(ESG) + a8(PPG) + a9(SHG) +
a10(G/SHOTS) + a11(PLSMIN) + a12(SAV) + a13(YEAR) + e

GA = a0 + a1LOG(TFW) + a2LOG(TFL) + a3LOG(PIM) +
a4LOG(G) + a5LOG(SAVPCT) + a6LOG(SHOTS) +
a7LOG(MAJORS) + a8LOG(YEAR) + e

The logs are used in the GA model "due to increased fit."

Right away, one glaring mistake stands out. To get useful results out of a regression analysis, you have to have independent variables (PIM, ESG, MAJORS etc.) that correlate highly with your dependent variable (PTS) but correlate minimally with each other. See caveat #5 here (pdf).

I.e. in hockey, it would be unwise to include, say, both 'total team salary' *and* 'team average age' as separate variables. One will surely be correllated with the other.

Your independent variables should not depend on one another. That's why they're called independent. Wikipedia calls this Multicollinearity. Multicollinearity is the source of "correlation, but not causation" effects. Other bloggers and hockey analysis websites have addressed this topic, but I'm too lazy to go looking for them.

Given that, how anyone could describe face-offs won and face-offs lost as separate, independent variables is beyond me. The authors of this paper do just that, and conclude that winning face-offs has a greater absolute effect than losing them:

"Thus, although TFW keeps an opposing team from scoring goals, TFL doesn’t necessarily imply a great chance for the opponent to score."

So, winning a face off is better than not losing a face-off. Impeccable logic. We're headed for the age of the high-event face-off man, who wins *and* loses more than 50% of his draws.

Of course, I picked out the most obviously interdependent variables to pick on but I think I made my point. Fighting majors could also correlate with one of the other variables. Other analyses have been done (again, too lazy to go look for them) that isolate the fighting majors and show that losing teams accumulate more of them than winning teams.

Reading the paper wasn't a complete waste of time. The most interesting line was in reference to a prior study by someone else whose results "...show that teams with unusually high or low numbers of French-Canadians tend to be less efficient." Unfortunately, that paper appears to be unavailable.

Rule 43

There is plenty of talk about head shots out there today, prompted by the "hard, but clean" hit by Torres on Williams.

Jim Kelley:

"When they apply that high-speed mass plus physical bulk and hard-shell equipment to an opponent's head, the results are near catastrophic. We saw that when Edmonton's Raffi Torres delivered his blow - by any hockey definition a "clean" check - to the head of Williams."

HNIC's Scott Morrison:

"Williams was emerging from the end boards, a few feet from the side of the Oilers goal, when Torres crunched with him a shoulder first check. Television replays showed Torres had built up a healthy head of steam, but stopped striding to avoid a charging penalty, then ran over Williams who appeared to be looking down at the puck."

Bob MacKenzie:

"If you hit him in the head, too bad, there's no rule against it and, in fact, it's tacitly endorsed by the league and the hockey community."

In every single piece discussing the hit, the writer goes out of his/her way to mention that it was clean. To be fair, the Mackenzie quote is lacking context. Bob was speaking from the perspective of those defending the hit.


Now, here's an excerpt from pages 93 & 94 of the Official NHL Rulebook:

" - Charging

43.1 Charging - A minor or major penalty shall be imposed on a player or goalkeeper who skates or jumps into, or charges an opponent in any manner.

Charging shall mean the actions of a player or goalkeeper who, as a result of distance traveled, shall violently check an opponent in any manner. A "charge" may be the result of a check into the boards, into the goal frame or in open ice.

...

43.2 Minor Penalty - The Referee, at his discretion, may assess a minor penalty, based on the degree of violence of the check, to a player or goalkeeper guilty of charging an opponent.

43.3 Major Penalty - The Referee, at his discretion, may assess a major penalty, based on the degree of violence of the check, to a player or goalkeeper guilty of charging an opponent (see 43.5).

43.4 Match Penalty - The Referee, at his discretion, may assess a match penalty if, in his judgement, the player or goalkeeper attempted to or deliberately injured his opponent by charging.

43.5 Game Misconduct Penalty - When a major penalty is imposed under this rule for a foul resulting in an injury to the face or head of an opponent, a game misconduct shall be imposed."

Contrary to popular belief, you don't have to be airborne to get called for charging. There is no 3-stride guideline, either. Going strictly by the book, Torres could have been given a major and a game misconduct. The check was violent, and the violence resulted from the distance traveled. After that, it's up to the discretion of the referee.

Which begs the question: If the Torres hit was not sufficiently violent to warrant a minor penalty, just how violent would a check have to be to warrant a major??


Some comments from Bobby Orr in the MacKenzie piece:

"Hey, I got hit a lot when I played and I didn't get hit in the head with checks. Players didn't always hit like that. To me, that's not part of bodychecking. I mean, don't you have to be responsible for your actions? If you hit a guy in the face with your stick by accident, you're going to get a penalty. Two minutes, four minutes, five minutes, something. If you go to bodycheck a guy and you hit him in the face or head, and injure him, that's legal? That's fair? That's not a penalty? I'm sorry, I don't think that is right. It should be a penalty."

It seems that the tools are already in place to crack down on hits like Raffi's. It's just a matter of whether there is the will.

Guillaumania!

Read all about it! The controversial remarks from former a former Hab great! What it's like to be the team's certain saviour! His rumoured romantic links to Jennifer Aniston! His secret feud with his estranged evil twin brother! His thoughts on Montreal media sensationalism!

~~~

Spector's most recent Soapbox gives up a peek at how Canada's provincial teams might stack up.

Wait a minute... where is New Brunswick? Led by the marginal Randy Jones and youthful Luc Bourdon and cheered on by Luc Bourdon, now of the Moncton Wildcats, Team NB could probably keep the score close when playing Dustin Penner's Team Manitoba.

~~~

How many concussions will Raffi Torres dish out before someone takes away his shoulder pads?

The guy is a bodychecking idiot savant. Check out his anticipation in the video of his hit on Jason Williams (courtesy of Off Wing). A goal scorer has an instinct for when and where the open ice and puck will converge. Torres has a knack for being at top speed at precisely the right time and place for a convergence of his shoulder and the puck carrier's noggin. As a kid, he must have been lethal in a bumper car.

Dang

Chris Higgins will be out for 6 weeks with ligament damage in his ankle.

As a crazed religious zealot once said, "When the hockey gods close a door, they open a window." Climbing in through the window tonight will be 19 year old Guillaume Latendresse, who will get his chance to play on the top line with Koivu and Ryder vs. the Oilers.

While I'm at it, here are all of the projected lines/pairings for the evening:

Latendresse - Koivu - Ryder
Samsonov - Kovalev - Perogy
Begin - Bonk - Johnson
Murray - Plekanec - Downey

Souray - Rivet
Markov - Komisarek
Streit - Niinimaa

Reflecting on this lineup, I must say that the Habs are doing OK at 7-3-3 while missing two of their regular defensemen for almost the entire season thus far.

~~~

Wow. This must be the geekiest Habs-related forum sig image ever.


Just in case the fan who created this image happens to be a regular reader: I'm laughing with you, not at you.

Goalies are Weird

First, there was the chain-smoking teammate in Bantam. Then there was guy on my intramural team in university whose shoulder kept "popping out," but who kept coming back to play in the same game. And then the former Network Security Officer I played with in an industrial league who was escorted off the premises by security for reasons unknown. The goalies that I have met have been a colourful bunch.

The Canadiens' goaltending coach (and former back-up) Rollie Melanson stays true to form. In a glowing Gazette article by Dave Stubbs, there are no quotes from Melanson at all. Apparently, he does not deal with praise very well.

Now for an anecdote. The parents of a buddy of mine live on the Eastern shore of N.B., not far from Moncton. Next door to them is Melanson's summer home. One fine summer day, these folks - let's call them the Jonses - were out doing some yard work when their neighbour pulled into his driveway. It soon became apparent that he was locked out of his house.

Mr. Melanson quickly became frustrated with his predicament. He scoured his landscaped yard for something, and seized a large rock. Mrs. Jones interrupted him before he could smash a window and invited him over until a locksmith could be summoned. Rollie the goalie sized her up, dropped his rock and said, "Fine."

Instead of following Mrs. Jones to her house, he turned around and walked to his car. He opened the trunk and pulled out a case of beer, and then walked next door. Once inside he set his case of beer on the coffee table, plopped down on the couch and started drinking in silence. When the locksmith arrived six beers later Rollie got up and left without saying goodbye.

Most hosts might have found this behaviour strange or even offensive. Fortunately, the Jonses are hockey fans and they understood completely.

The next bit of former netminder weirdness comes from Kelly Hrudey. In this article, Hrudey candidly discusses the on-air puff-piece that is the After Hours segment of HNIC before dropping the bombshell that he will be interviewing former president Bill Clinton on Friday. How many serious journalists - veteran ones at that - have been trying for years to get this kind of opportunity? It certainly bodes well for my own personal "Kelly Hrudey should replace Don Cherry" campaign.

~~~

Dig deep, folks, for the Craig MacTavish Relief Fund. You have until Wednesday. In all likelihood, the money will go toward a very good cause - the CNIB. If I had my druthers, I'd put it toward a copy of "Hockey for Dummies" and a good stationary bike for Mick McGeough.

~~~

Naturally, I had to read a blog entry by an Albertan to find out about a mention of Sisu Hockey in the French mainstream media. Wow! I'll celebrate by providing a link to this very entertaining essay. That ought to scare off the tourists.

Housekeeping

One never really knows housekeeping until one is married.

Links added:
the hockey recap (a fantastic one-page resource for poolies)
Team Salaries & Contracts
NHL on Google Video

Blogs added (some long overdue - there is getting to be too much great content out there for me to keep track):
American Hockey Fan
BFLO blog
Lowetide
The Hockey Chick
More Hockey Less War
Southeast Shootout
Two for Elbowing

Blogroll Updates:
Abel to Yzerman is now available over at Kukla's Korner.
Behind the Jersey relocated months ago.
James Gunner is now at 8feet.
Finally, I added that little squiggly thing over the ő in Gőlbez.

~~~

Last night, Marian Hossa had 16 shots on goal and Ilya Kovalchuk had 16:35 of power play icetime in a 5-2 loss to the Hurricanes. At one point in the game, Carolina had 20 PIMs to Atlanta's 6. Bet that was fun to watch.

Habs Hallo-WIN

Puns rock.

Last night, a trick-or-treater dressed as a witch stepped out of the shadows and onto our doorstep carrying a Montreal Canadiens pillowcase. I offered the mysterious stranger double treats if she would cast a hex on the Ottawa Senators. She obliged. The result: 4-2 Habs.

If you missed the game, the score is quite misleading. It was actually a 2-1 game with three Bettman-mandated extra goals in the dying moments to give the illusion of a higher-scoring contest.

Radek Bonk deserves props. Aside from the brief cranial paralysis for the Sens' first goal, his line did a hell of a job smothering Spezza/Heatley. Under yet another coach (the third he has seen with the Habs), he keeps getting big defensive minutes. The Bonk-Johnson tandem has been a solid plus producer - they are both on pace for a +37 season.

Once you get past your preconceived notions that he should score more because of his high draft position, you discover that he's a pretty good player.

Johnson has put up 7 points and a +5 in 11 games in a checking/PK role. Jan Bulis has 6 points and a +1 in 13 games in a scoring/PP role with the Canucks.

~~~


Over at Tom Benjamin's the comments are always a great read.

This one by 'cambo' really got my goat:

"Fans are sheep who thrive on the manure the media feeds them about "greedy players." Even in a city like Edmonton, where the former owner sold Gretzky and broke up the dynasty, fan support during the recent labor strife was 100% behind ownership. Not one of those idjit fans, I guarantee, was told at 18 where he MUST move to ply his trade and that he wouldn't have a choice in the matter until at least the age of 25."

It's not an original remark. This hardcore libertarian attitude was prominent during Prongergate, too.

So, "how dare they dictate where a guy plays from the age of 18 to 25?"

Answer: they don't.

The workplace restrictions apply to NHL draftees who choose to play in the NHL. The players have a choice. Any draftee can eschew the chance to play in the NHL and take up welding or computer programming if they like. Or even go play in another league.

The NHL sells competition. For it to be competitive, it must have some restrictions on player movement. If it's a pure free market, it's going to look like most beer leagues where a good chunk of the best players gather on one team. In a pure free market, why would a star choose a city with higher taxes (like Montreal)? Or an obtrusive media (like Montreal)? Or to a team that sucks (like... Phoenix)?

In the same discussion, this question is posed:

"How do the Pens cope with Crosby/Malkin/J. Staal/Fleury?"

Answer: they don't.

The salary cap prevents anyone from amassing a dominating collection of talent. The best you can do is assemble a pretty good contender. If the math prevents you from having a great, 130-point team for a handful of seasons, the wise move would be to shuffle your assets so you have a 100-point team for a decade. The Pens would be wise to move some of that potential greatness for some long-term goodness before they inevitably lose it to free agency.

There will always be a trading partner willing to give up future for present. In the old paradigm it was the bad, rebuilding teams who traded for the future. Now, the very good teams with more assets than cap space should trade for the future too.