In Defense of the Low-Event Players
I made a spreadsheet today. Given a GF/game and a GA/game rate, it simulates the results of 1000 games.
The rates are divided by 60. Then each game is simulated in 60 sections. A different random number is compared to each rate each minute. When the GF random number is lower than the GF/minute rate, a goal for is counted for that minute. Same goes for the GA. The GF and GA are totalled up after 60 minutes to produce a game score. If the score is tied at the end of 60, it is counted as a tie.
I had a couple of objectives. First, I wanted to test my belief that a given positive goal differential is more meaningful in a low-scoring environment than in a high-scoring environment.
I ran the simulation for ten times for a total of 10,000 games for six different GF/GA rate pairings.
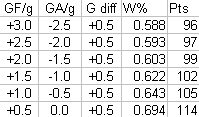
The pts column is simply the number of points this w% would correspond to in an 82-game season.
The difference is not as pronounced as I expected. This is probably due to the increasing liklihood of ties in low-scoring games.
Secondly (and more importantly), I wanted to test the effects of situational changes to a team's GF/GA rates mid-game. To do this, I set up columns for running game scores with initial GF/GA rates (i.e. +3.5/-3.0), and more conservative GF/GA rates (i.e. +1.0/-1.0).
Then I added a hybrid column that started out with the 'initial' GF/GA rates. When the team had a lead, they would switch to the conservative rates. If they were tied or behind, they would switch back to their initial game plan.
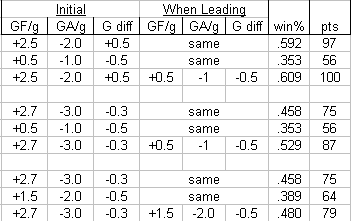
In the first example (first three rows of the table), the team plays initially with GF/GA rates of +2.5/-2.0 for a goal differential of +0.5. Playing this way all the time would lead to a .592 win%. This team can also play a shut-down style, producing +0.5/-1.0. If they played this way all the time, they would have a win% of .353.
However, if this team started out with their first rate, then switched to their shut-down rates whenever they had a lead, their win% jumped to .609. There are situations when a negative goal differential can be better than a positive goal differential.
This is a dumb simulation, too - if the team took a 1-0 lead in the first minute, it would unwisely switch to the low rates until the opponent tied it up. If it were built to gradually change to the most defensive style or only do so in the 3rd period, it would probably produce even better results.
In the second and third examples the effect is more pronounced. At it's best, this team can only produce a +2.7/-3.0 for a differential of -0.3. They can play the same shutdown style as the first team, +0.5/-1.0. Although both styles produce a negative differential, when used in unison they can produce a winning team. Weird.
In the third example, the team's initial rates are +2.7/-3.0 again, but can only manage +1.5/-2.0 when playing defensively. I added this option in case a +0.5/-1.0 style is beyond the realm of possibility. Even so, the team sees improvement when switching to the lower-event style although it has an worse differential than their initial gameplan.
So, it is provable that going into a defensive shell has merit. When you're leading, it can be wise to sacrifice two goals from your GF/game rate if it means you can reduce your GA/game rate by one. However, it's not so easy to prove that the defensive games some teams employ actually reduces their GA/game rate significantly.
Also worth mentioning - this simulation only considered one team who could change their style of play. If the team in question fell behind they could still score at their higher rate, giving them an advantage. A more realistic simulation would consider changes to the opponent's style of play as well.
There is a flaw in this simulation technique: The win probabilities are a little low compared to what should be expected (pdf). I believe that could be corrected by tinkering with the sample rate and I don't think this bug should invalidate my conclusions, but I certainly could be wrong (any input, stats gurus?)
In Conclusion
Most statistical analyses break the game up into even strength, PP and PK situations. I think it's clear that game situations - tied, leading, trailing - should also be considered. Players are not robots who simply produce goals for and against at a fixed rate in a Poisson-like distribution regardless of the score. Even if you're a solid plus player against any opposition, it's not smart to play gung ho for the greatest positive goal differential. There are times when a lower GA style - even at the expense of a negative differential - is the preferred way to play. Of course, this is entirely contingent on whether it is even possible for teams/players to change their style in this manner. It's not a given that this is possible. If it is possible and done regularly, then playing when ahead/behind can be a very different game than playing when tied - just like playing on the PP/PK is a different game than playing at ES. I'd be very interested to see stats listing the most effective players in tied game situations.
Now, if you accept that playing low-event game is wise when leading, it also stands to reason that it would be wise to change one's style to a higher-risk game (more GF at the expense of far more GA) when losing games. You see this regularly with pulled goalies.
P.S. This all reminds me of a good discussion over at Tom Benjamin's awhile back (sorry - can't find the exact post) about the relative effectiveness of Ohlund and Jovanovski under different situations. Ohlund was used more when the Canucks were leading while Jovo played more when losing. Jovanovski incurred some additional minuses due to playing a riskier style uinder these circumstances. This made him look bad statistically, but really had a minimal effect on the team's record since they were already losing. It's an excellent illustration of what I'm trying to say in this post.
~~~
Speaking of low-event...
0-0 tie last night. Although no individual player scored any points, the NHL standings system sees fit to distribute three points amongst the teams involved.
The rates are divided by 60. Then each game is simulated in 60 sections. A different random number is compared to each rate each minute. When the GF random number is lower than the GF/minute rate, a goal for is counted for that minute. Same goes for the GA. The GF and GA are totalled up after 60 minutes to produce a game score. If the score is tied at the end of 60, it is counted as a tie.
I had a couple of objectives. First, I wanted to test my belief that a given positive goal differential is more meaningful in a low-scoring environment than in a high-scoring environment.
I ran the simulation for ten times for a total of 10,000 games for six different GF/GA rate pairings.

The pts column is simply the number of points this w% would correspond to in an 82-game season.
The difference is not as pronounced as I expected. This is probably due to the increasing liklihood of ties in low-scoring games.
Secondly (and more importantly), I wanted to test the effects of situational changes to a team's GF/GA rates mid-game. To do this, I set up columns for running game scores with initial GF/GA rates (i.e. +3.5/-3.0), and more conservative GF/GA rates (i.e. +1.0/-1.0).
Then I added a hybrid column that started out with the 'initial' GF/GA rates. When the team had a lead, they would switch to the conservative rates. If they were tied or behind, they would switch back to their initial game plan.

In the first example (first three rows of the table), the team plays initially with GF/GA rates of +2.5/-2.0 for a goal differential of +0.5. Playing this way all the time would lead to a .592 win%. This team can also play a shut-down style, producing +0.5/-1.0. If they played this way all the time, they would have a win% of .353.
However, if this team started out with their first rate, then switched to their shut-down rates whenever they had a lead, their win% jumped to .609. There are situations when a negative goal differential can be better than a positive goal differential.
This is a dumb simulation, too - if the team took a 1-0 lead in the first minute, it would unwisely switch to the low rates until the opponent tied it up. If it were built to gradually change to the most defensive style or only do so in the 3rd period, it would probably produce even better results.
In the second and third examples the effect is more pronounced. At it's best, this team can only produce a +2.7/-3.0 for a differential of -0.3. They can play the same shutdown style as the first team, +0.5/-1.0. Although both styles produce a negative differential, when used in unison they can produce a winning team. Weird.
In the third example, the team's initial rates are +2.7/-3.0 again, but can only manage +1.5/-2.0 when playing defensively. I added this option in case a +0.5/-1.0 style is beyond the realm of possibility. Even so, the team sees improvement when switching to the lower-event style although it has an worse differential than their initial gameplan.
So, it is provable that going into a defensive shell has merit. When you're leading, it can be wise to sacrifice two goals from your GF/game rate if it means you can reduce your GA/game rate by one. However, it's not so easy to prove that the defensive games some teams employ actually reduces their GA/game rate significantly.
Also worth mentioning - this simulation only considered one team who could change their style of play. If the team in question fell behind they could still score at their higher rate, giving them an advantage. A more realistic simulation would consider changes to the opponent's style of play as well.
There is a flaw in this simulation technique: The win probabilities are a little low compared to what should be expected (pdf). I believe that could be corrected by tinkering with the sample rate and I don't think this bug should invalidate my conclusions, but I certainly could be wrong (any input, stats gurus?)
In Conclusion
Most statistical analyses break the game up into even strength, PP and PK situations. I think it's clear that game situations - tied, leading, trailing - should also be considered. Players are not robots who simply produce goals for and against at a fixed rate in a Poisson-like distribution regardless of the score. Even if you're a solid plus player against any opposition, it's not smart to play gung ho for the greatest positive goal differential. There are times when a lower GA style - even at the expense of a negative differential - is the preferred way to play. Of course, this is entirely contingent on whether it is even possible for teams/players to change their style in this manner. It's not a given that this is possible. If it is possible and done regularly, then playing when ahead/behind can be a very different game than playing when tied - just like playing on the PP/PK is a different game than playing at ES. I'd be very interested to see stats listing the most effective players in tied game situations.
Now, if you accept that playing low-event game is wise when leading, it also stands to reason that it would be wise to change one's style to a higher-risk game (more GF at the expense of far more GA) when losing games. You see this regularly with pulled goalies.
P.S. This all reminds me of a good discussion over at Tom Benjamin's awhile back (sorry - can't find the exact post) about the relative effectiveness of Ohlund and Jovanovski under different situations. Ohlund was used more when the Canucks were leading while Jovo played more when losing. Jovanovski incurred some additional minuses due to playing a riskier style uinder these circumstances. This made him look bad statistically, but really had a minimal effect on the team's record since they were already losing. It's an excellent illustration of what I'm trying to say in this post.
~~~
Speaking of low-event...
0-0 tie last night. Although no individual player scored any points, the NHL standings system sees fit to distribute three points amongst the teams involved.


1 Comments:
Ok after the tonight game i think we dont need to sign Rivet and Sourray no more....
Post a Comment
<< Home